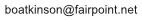multiple-hedron-tetrahedrons
Regular polyhedron solids are reticulated as a series of explorations in natural geometry, growing outwardly according to patterned sequences. The basic concentric outgrowths have primarily involved edge and vertex attachments, but this page combines edge and face attachments of the tetrahedron.

Concentric multiplexing of regular, centered tetrahedra will face-attach copies of tetrahedrons and rotationally scale them, sequencing added layers outwardly, concentrically and symmetrically.

Hundreds of tetrahedra have been clustered in these models and a question of structure is noted as to whether individualized polyhedra should be unitized as one volume, as one geometrical object or should all attachments remain individual, (as indicated by coloring in the image above), and another question is whether face, vertex and/ or edge attachments remain segregated or become integrated in the generated products. Geometry apps allow any of these approaches, which introduces new generic questions about definitions and nomenclature.

This “100s model” above is built out with face-to-face attachments, (unlike the other types of polyhedra in this series of 3d models). The procedure can vary in kinds of transformations and the multi-hedronTet starts out with edge attachments and next level switch to face attachments. The term of level-multiplex attempts to account for sequenced levels as other polyhedral models in the series have not included face to face attachments.

Rota-scalar-plexed as a term attempts to summarize the general process of rotating, scaling and multiplexing polyhedral objects. Sequencing multiple-rota-scalar-plexed events outwardly adds concentric layers to a multiplex structure .
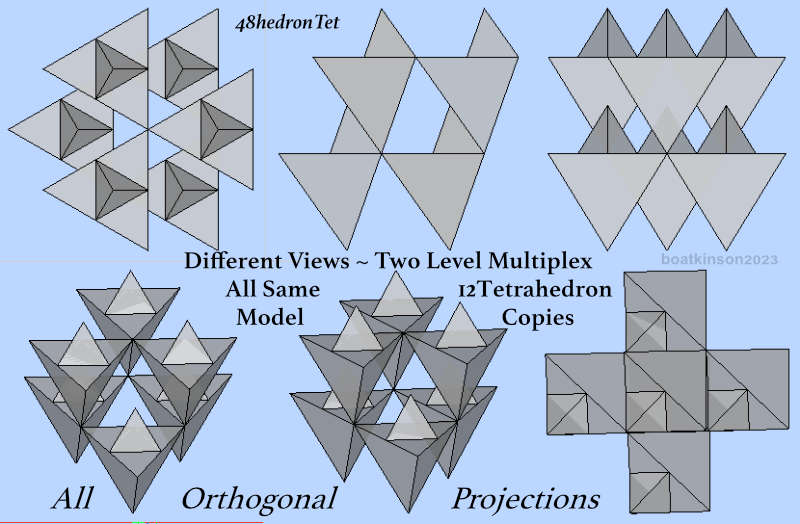
A variety of resulting outlines and 2d profiles have been found in this same three level model, with tetrahedral multiplexing, (of unchanging and regular sequencing), and has generated the most variety of 2d forms. Sort of a 3d cross branches out in six directions.
Patterning of attached-sequences provides would be 3d explorers a lot of opportunities in discovering previously unseen forms which are entirely natural outcomes of geometry, with computer precision .
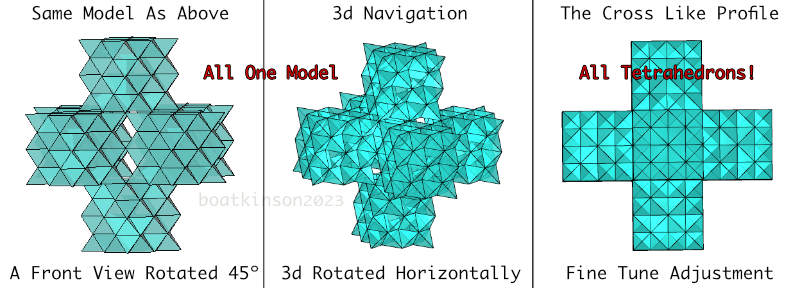
The first tetrahedral stellated pattern surprisingly developed into a “vector equilibrium matrix” which is not a regular polyhedron, and the method began with face attachment to a tetrahedron and finally ended up with vertex-to-vertex attachments in the next image below. On the left, orthographic projections of the result associate the tetrahedral seed with the fruiting of a cube; whereas, the perspective projection, (or wide angle lens) render a spherical form:
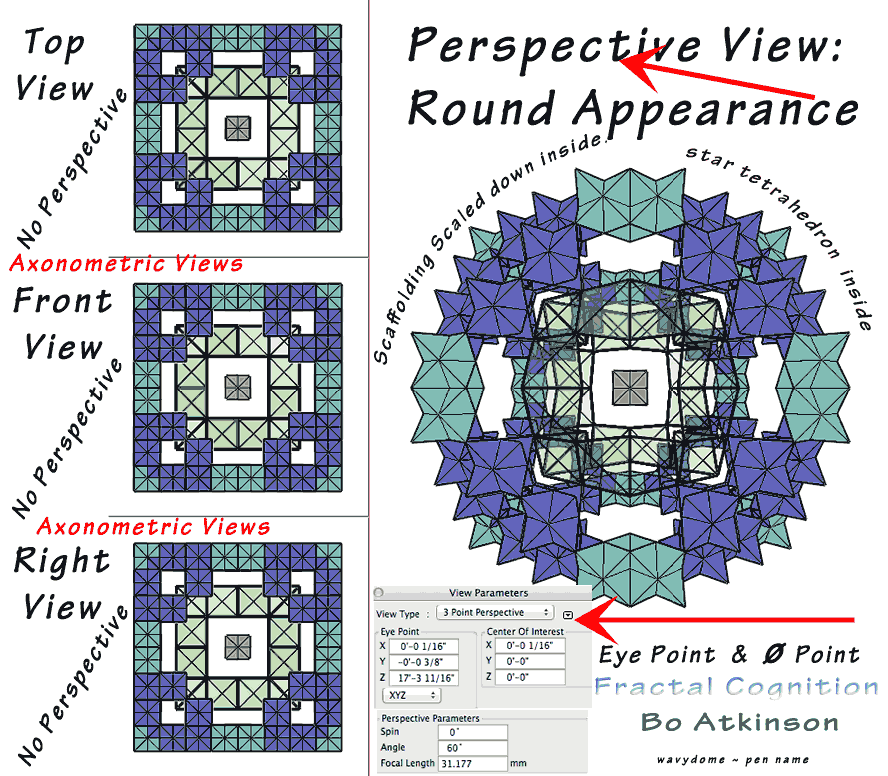
At first this work focussed on the outward growth of polyhedra, while the inverse products of the foregoing processes are separate, still just works in progress.
Multiplexing tetrahedrons was generically inspired by many creative individuals internationally and by a variety of naturally occurring architectures as well.
Next is the earlier sequence of the model above. A layout of the same views generally exposes a signature outline, found to repeat itself in subsequent levels, except and unless other rule-patterns of construction are used.
http://harmoniouspalette.com/FractalStarCoil.html
http://harmoniouspalette.com/StartetrahedralCircuitAssembies.html
http://harmoniouspalette.com/StartetrahedralCircuitAssembies.html