
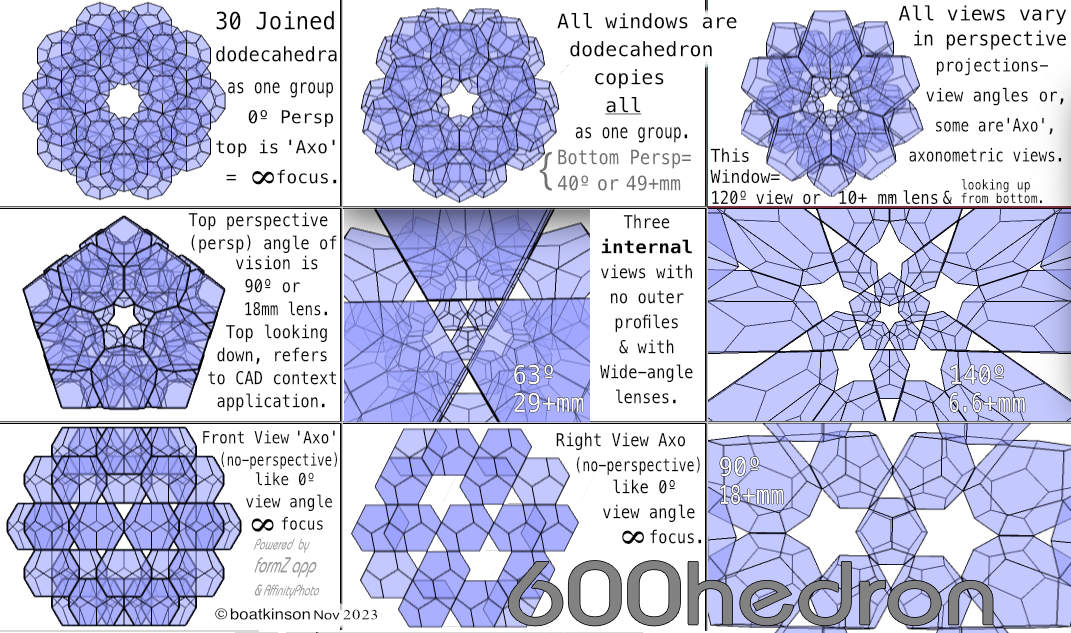
Thirty dodecahedra, each composed of twenty regular faces count as six hundred faces or -hedra or hedrons. The process is like networking or multiplexing dodecahedra concentrically.
A series of 3d computer models discovered that the same number of -hedrons could result in differing regular or Platonic solids; therefore, name experimentation aimed to clarify what specific structures.
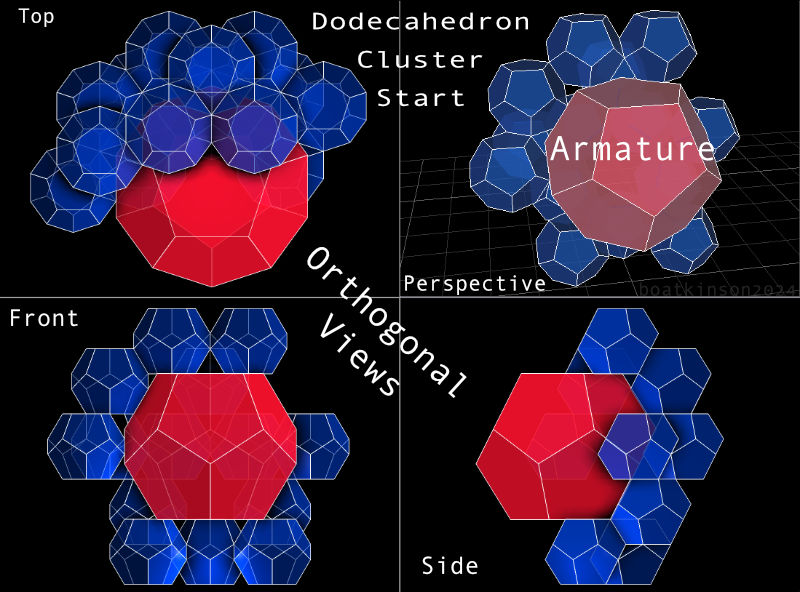
Originally, matching face counts was not anticipated nor was the possible expansion of the series. Also the five main tools used for these presentations were very difficult to coordinate and this model was mistakenly counted wrong, as 360 faces, resulting in the mistaken name 360hedron.
This Image = 1071 X 633
Thirty dodecahedrons have been grouped together as facetted geometry, and grouped as a somewhat spherical outer form, where edges meet. The general form can be made into one object which will then consist of 600 identical faces, because 30 dodecahedrons X 20 faces each = 600 faces total.
So called Xray image below is also called a wire-frame rendering in 3d apps, but it was also later-photo-edited with a luminescent layer added beneath the lines.
Precise rendering of regular Platonic solid clusters offer sufficiently patterned details to ponder rewardingly.

It makes sense that segments joining in polyhedra could be substituted with the rightly proportioned polyhedron of the same kind meet and join together as one object. Or alternatively consider them as independent objects just touching, as at first these arrive together individually.
This process soon inspired a notion of repeatedly multiplexing resulting aggregations together, and deriving other kinds of geometry as well. Publishing those results will take longer and will be shared later.

These stars suddenly jumped out as the routine render settings were adjusted, and the main revealer of stars was union-ing all dodecahedrons into one object. Brightening the lights and reducing the shading also reveals stars.
This outcome was an unexpected surprise, that the same model discussed on this page, identically composed, should reveal stars inside of a cluster of dodecahedrons, and only due to mathematically rendered properties.
Next most of the dodecahedrons were removed to determine how many were needed to render a star.
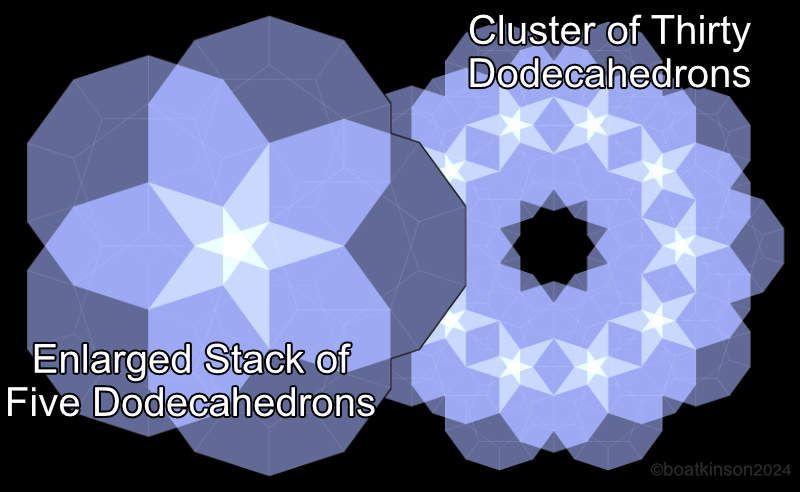
It turned out that five vertically positioned and attached dodecahedra are required to form stars, edge attached and ‘stacked’. “Shader rendering has been used for all the multiplexed polyhedrons in this series.
Next are isolated two ‘stacks’ of decahedrons which belonged tot the cluster of thirty, (introduced above). The dodecahedron stack of individualized dodecahedra is compared with a stack of union-ed dodecahedra made into one volume, (one object).

Next is an enlarged image of one ‘stack’ of five dodecahedrons superimposed over the clustered of 30, and the image of five suggests a third star is revealed, but it is lost when clustered in the 3d concentric multiplex. Singled out it may be considered as three stars.
More additions and edits for clarity may follow.