
240vertexhedrons
Twenty dodecahedra have been attached together as facetted geometry, and grouped as a somewhat spherical outer form, where edges meet. The general form can be made into one object which will then consist of 240 identical faces.
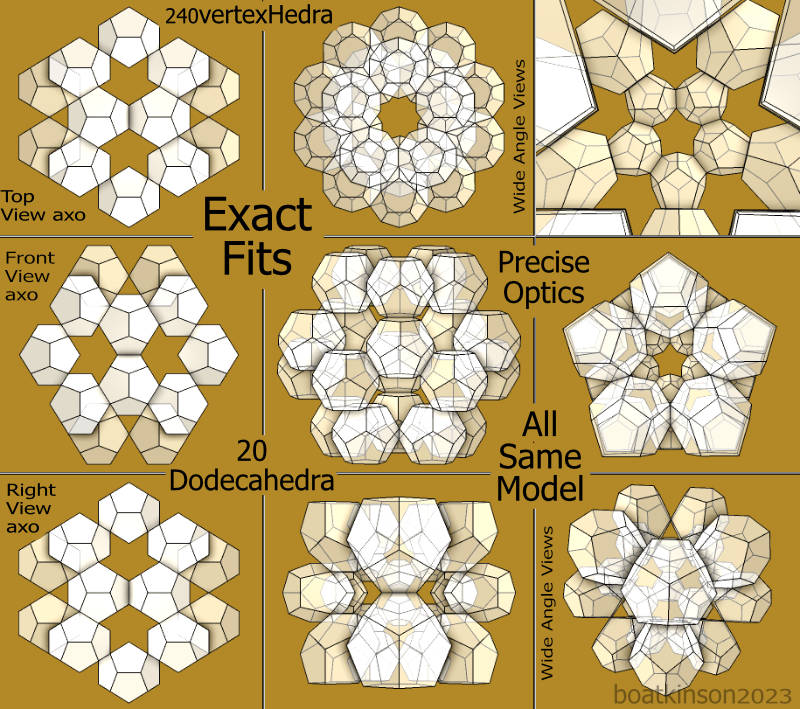
It makes sense that segments joining in polyhedra could be substituted with the rightly proportioned polyhedron of the same kind, meet and share on volume all together as one object. Or just leave them as independent objects just touching, as at first these arrive together in that way.
This was thought up in advance as an exploration to see what would result. Instead of thinking about an equation to solve the structure, a physicalist approach was taken.
All of these 2d renderings reveal different angles and lighting of one structure.
Objects or structures in architectural and engineering apps are primarily 3d projects which display on 2d screens or prints, yet actually present all the measured facts of objects or structures. These are potential builder plans in physical life, (ready or not).
Next image focuses on semi transparent faces and edges, and without shading included.
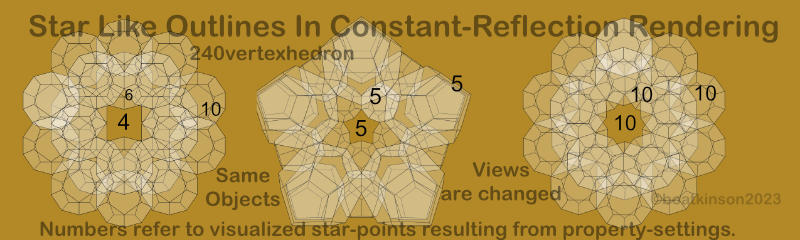
Joining all touching volumes into one unified volume might be considered as unserviceable, but these structures are entirely buildable in real life, and not arbitrarily random. Generic classes of these structures can be sorted out to study the the numeric sequences, and for testing new-found applications of sequences. Additional orientations of polyhedra yet remain to model and extend the numerical relationship data.
Concentric multiplexing of a regular, centered polyhedron will attach like -hedrons which are center-edges-to-center-edge, vertices, faces, or combinations of these, and alternatively, rotationally-scaling, to mathematically match, by generating the correspondingly arranged -hedrons of equivalent properties. The central armature is not counted in the focus on outward-structuring.
The idealist is free to hypothesize unity of structural aspects and numerical relationships.
Originally, the 240hedon and 360 hedron were modeled by moving and snapping center points placements of smaller sized dodecahedra with a tool which cloned each copy as it was moved into place. Following that, just one dodecahedron was upscaled in size as all copies simultaneously grew in size. The manual scaling tool could simply click on the midpoint of the activated tetrahedron and drag it towards the approaching cloned- dodecahedron, (to snap on its midpoint).
Next is appended another and less complex class of face-attached -hedrons, contrasting the vertex-attached and edge attached. Twelve dodecahedra add up 144 faces or -hedrons, and lesser detail of fewer faces present less 2d patterning to explore.
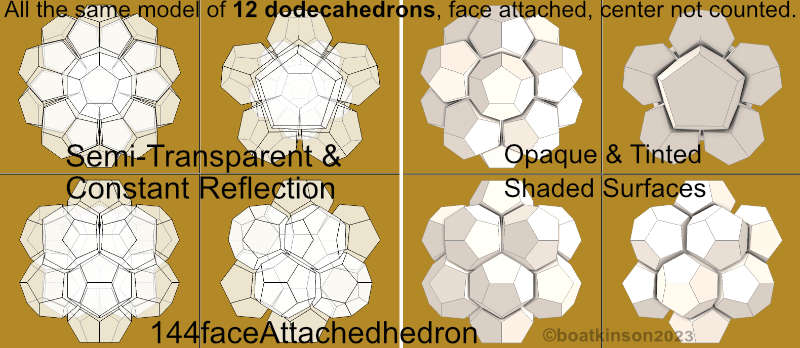
Each face has an attached copy of the central dodecahedron we have called the armature, as it defines the exact placements, and in this case five edges of each dodecahedron match and attach to five other edges of the the structure.
Even the less complex 144faceattachedhedron contains some similarities, while its simpler outline retains the nearly spherical profile. An 8mm+ lens, or very wide angle view zoom just inside one face of the 144 outer-faces. A flower like look is suggested, and one star traces around the 'leaves'. Another ten point 'star' almost traces around the plain pentagons near center.

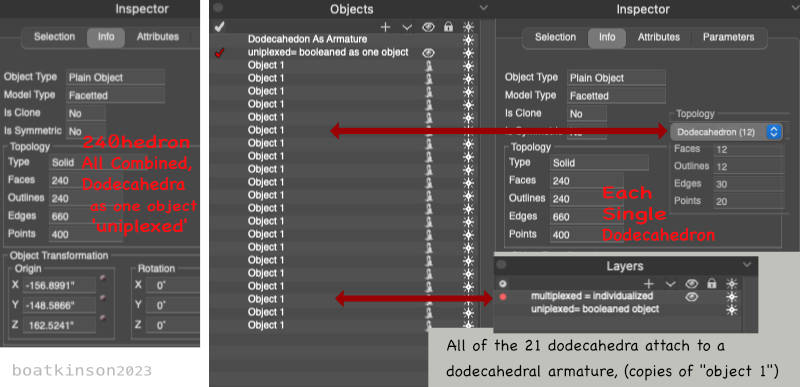

Geometrical modeling of parameterized objects can shift internal code content which might demand continued verifying with an inspector tool. Mentation of structure may simply focus on the principles of geometric rules, realizing that “transformed polyhedra” can be edited back into parametrized polyhedra, which is manual labor given a compelling reason to do so.
There are many options, settings and layouts to adjust as the modeling intends to assure accuracy of outcomes. A user-interface inspection could look like this, but is typically more scattered than is needed in this kind of workflow.

Concentric multiplexing of a regular, centered polyhedron will attach mutual -hedrons symmetrically, and alternatively with rotational scaling to generate the mutually touching sets, with mathematical precision.
